Black Body Radiation and The Ultraviolet Catastrophe: The Birth of Quantum Mechanics
Sam Veiner – April 14 2025
Our understanding of the physical world took a significant blow with the birth of Quantum mechanics, a relatively new realm of physics.
A black body is an idealized physical object that absorbs all electromagnetic radiation regardless of frequency or angle. When heated, it emits thermal radiation across all wavelengths. All mass emits thermal radiation, but a black body emits all possible wavelengths of light, which are dependant only on the its temperature, and absorbs all incoming light.
Stars, despite being far from ‘black’ are some the closest objects in the universe to an ideal black body, due to low reflectivity and wide spectrum of electromagnetic radiation.
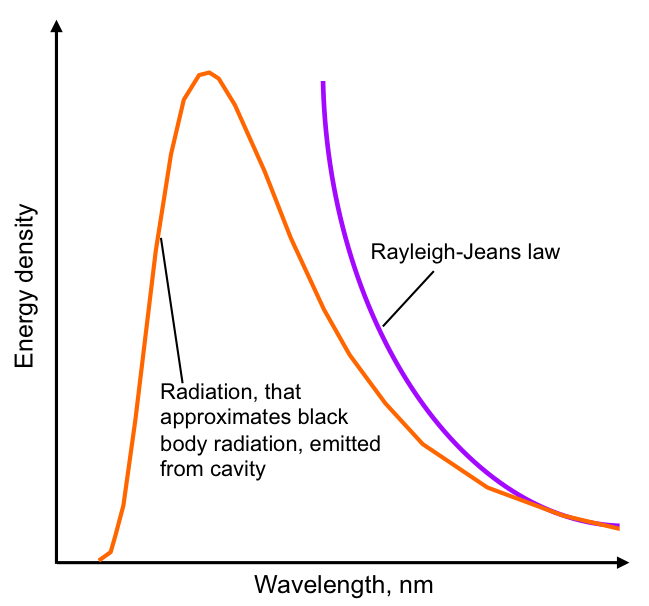
The black-body problem was approached by classical physics with the Rayleigh-Jeans law, which states the intensity of radiation emitted by a black body should increase without limit as the incoming wavelength decreases (frequency increases). Classical physics predicted that: Real objects should emit infinite energy at high frequencies – as you move toward higher frequencies (ultraviolet, X-rays, etc.) Energy output should approach infinity. This absurd conclusion was dubbed the “ultraviolet catastrophe” because the mathematical model catastrophically failed in the ultraviolet region and beyond. in practice, energy intensity decreases after reaching a maximum intensity, contradicting the classical interpretation of a black body. A new atomic understanding was needed to resolve the problem.
In 1900, Max Planck solved the problem by proposing that radiative energy is released in discrete packets, or quanta. Those packets would later be defined by Einstein as photons. Plank proposed that radiation is not continuous, rather released in blocks of energy.
Planck stated that the energy of a photon is proportional to its frequency. E=hf (energy = Planck’s constant times frequency) This quantization creates a crucial effect: As frequency increases, it becomes increasingly unlikely for a quantum of energy to be emitted, therefore solving the ultraviolet catastrophe. This happens for the following reasons:


- At higher frequencies, each photon requires more energy (E=hf)
- The thermal energy available to create these quanta is limited
- The probability of emitting a quantum follows an exponential distribution, given by the Boltzmann factor calculated by Ludwig Boltzmann, where the chance of emitting a photon exponentially decreases in likelihood with an increase in frequency.
The Planck and Boltzmann solution to the ultraviolet catastrophe were the first discoveries in the realm of quantum physics, which was named after the discrete nature of energy and other behaviors of atomic and subatomic scale physics.